图

无向图

无向图---->无向边(边)  (v,w)=(w,v)   E={(A，B),(B,C),(C,D),(D,E)}
度：依附于顶点的边的条数 TD(v)
无向图全部顶点的度的和为边数的二倍
无向完全图有n(n-1)/2条边

有向图

有向图---->有向边(弧)    <v,w>!=<w,v>   E={<A,B>,<B,C>,<C,D>}
入度：以顶点为终点的弧 ID(v)
出度：以顶点为起点的弧OD(v)
度：入度和出度的和TD(v)
在有n顶点，e条边的有向图中，所有顶点的ID和OD的和等于e
有向完全图有n(n-1)条弧

简单图

1.不存在重复边
2.不存在顶点到自身的边

多重图

1.图中某两个节点间的边数多于一条(有向图互相指不算，需要为同向的)
2.顶点与自己相关联

顶点和顶点间的关系

1.路径：从点A到点D的顶点序列 eg.A-B-C-D （路径也是有向的）
2.回路（环）：第一个顶点和最后一个顶点相同的路径
3.自环
3.简单路径：路径中顶点不重复出现
4.简单回路：除第一个顶点和最后一个顶点外，其余顶点不重复出现
5.路径长度：路径上的边数
6.点到点的距离：从A到D的最短路径若存在，则称最短路径为A到D的距离，若A到D不存在路径则距离为无穷
7.连通：无向图中 A到D有路径则为连通  若每个顶点都连同则为连通图 
n个顶点的无向图G 若G为连通图，最少有n-1个边 若为非连同图，最多有C 2 n-1条边
8.强连通：有向图中 A和D间正向反向路径均存在则为强连通 若任何一对顶点均为强连通则为强连通图
n个顶点的有向图G 若G为强连通图，则最少有n条边（形成回路）

存储结构

邻接矩阵

Aij
两点之间有边则为1，反之为0
两点间有权值则为权重，i=j时为0，否则为无穷

邻接表

对图中每个顶点建立一个单链表，存储该顶点所有临界顶点及其相关信息

图的遍历

BFS(广度优先遍历)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

//O(n*n) 基于邻接矩阵的bfs，仅适用于顶点为int型的
queue<int> q;
void bfs(int s){
	cout<<s<<" ";  //输出当前顶点信息
	visit[s]=1;    //标记当前顶点已被查询
	q.push(s);     //入队
	while(q.size()){//若队不为空
		int t=q.front();//出队
		q.pop();
		for(int i=1;i<=n;i++){ 
			if(visit[i]==0 && a[t][i]==1){
				cout<<i<<" ";
				visit[i]=1;
				q.push(i);
			}
		}
	}
}

//O(n+m)基于邻接表的bfs
queue<int> q;
void bfs(int s){
	cout<<s<<" ";
	visit[s]=1;
	q.push(s);
	while(q.size()){
		int t=q.front();
		q.pop();
		for(int j=0;j<a[t].size();j++){
			int v=a[s][j];
			if(!visit[v]){
				cout<<b<<" ";
				visit[b]=1;
				q.push(v);
			}
		}
	}
}

DFS(深度优先遍历)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//O(n*n)基于邻接矩阵的dfs
int a[N][N] ;
int n,m;
bool visit[N];//标记数组 
void dfs(int s){
	cout<<s<<" ";
	visit[s]=1;
	for(int i=1;i<=n;i++){
		if(!visit[i]&&a[s][i]==1){
			dfs(i);
		}
	}
}

//O(n+m)基于邻接表的dfs
vector<int> a[N];
int n,m;
void dfs(int s){
	cout<<s<<" ";
	visit[s]=1;
	for(int j=0;j<a[s].size();j++){
		int v=a[s][j];
		if(!visit[v]) 
			dfs(v);
	}
}

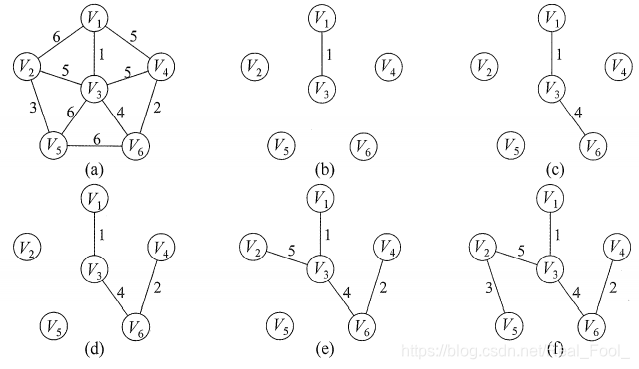
最小生成树

普里姆(Prim)算法

算法原理

初始时从图中任取一顶点(如顶点加入树T，此时树中只含有一个顶点，之后选择一个与当前T中顶点集合距离最近的顶点，并将该顶点和相应的边加入T，每次操作后T中的顶点数和边数都增1。以此类推，直至图中所有的顶点都并入T，得到的T就是最小生成树。此时T中必然有n-1条边
prim

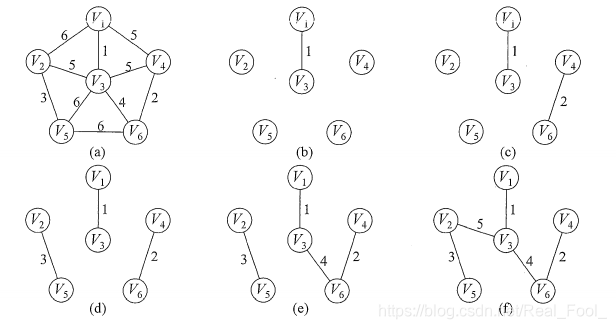
克鲁斯卡尔(Kruskal)算法

算法原理

初始时为只有n个顶点而无边的非连通图T = V , T= {V, {}}T=V,，每个顶点自成一个连通分量，然后按照边的权值由小到大的顺序，不断选取当前未被选取过且权值最小的边，若该边依附的顶点落在T中不同的连通分量上，则将此边加入T，否则舍弃此边而选择下一条权值最小的边。以此类推，直至T中所有顶点都在一个连通分量上
kruskal

两者区别

c

最短路径

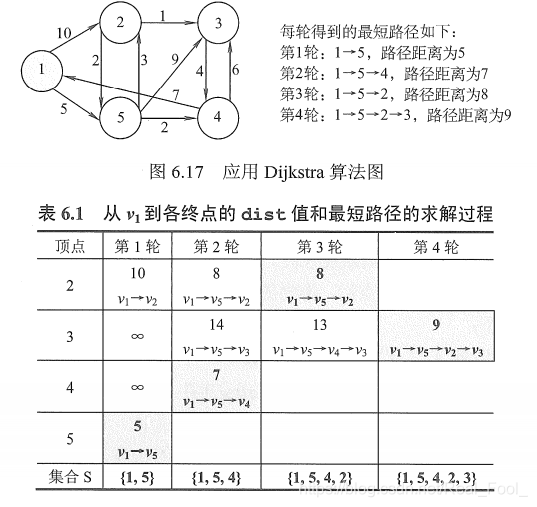
迪杰斯特拉(Dijkstra)算法

算法原理

单源最短路径，从一个点出发，每次选最近的边权值最小的点，然后更新
dij

Floyd(弗洛伊德)

算法原理

邻接矩阵存图，两个二维数组，D和Path。D记录最短路径权值，不连通为0；Path记录最短路径终点的前驱，自己到自己或无通路为-1
依次将每个点作为中间点递推做更新,以谁作为中间点，相应下标的行和列的路径值不变
对n个顶点的图G，任求一对顶点Vi->Vj之间的最短路径可分为以下几个阶段：
#初始 D为初始邻接表，Path根据图写
#第0 若允许在V0中转，最短路径
#第1 若允许在V0，V1中转，最短路径
#第n-1 若允许在V0,V1…Vn-1中转，最短路径