第六章

关系模式表示

五元组 R(U,D,DOM,F)

R是元组名（学生）
U为属性（学号，姓名，专业）
D为属性的域（整数，字符串，字符串）
DOM为属性到域的映射（001，李明，计算机）
F为属性上的数据依赖

数据依赖：

函数依赖（FD）

有R(U)，设X，Y为U的子集，若对于R(U)的任意一个可能的关系r，r中不可能存在两个元组在X上属性值相同，而在Y上属性值不同，称X->Y（X决定Y，Y依赖于X）

下表不属于函数依赖，因为两个元组学号相同但是姓名不同

学号	姓名
001	张三
001	李四

函数依赖类型：

非平凡函数依赖
X->Y，但Y⊊X，则称X->Y是非平凡函数依赖（本身推其他）
平凡函数依赖
X->Y，但Y⊆X，则称X->Y是平凡函数依赖（本身推本身）

完全函数依赖
如果X->Y，并且对于X的任意真子集X’，都有X’-/->Y，则称Y对X完全函数依赖，写做X-F>Y（若不存在子集则一定是完全函数依赖）
部分函数依赖
如果X->Y，但Y不完全依赖于X，则称Y对X部分函数依赖，记作X-P>Y

传递函数依赖
如果X->Y(Y⊊X)，Y-/->X，Y->Z(Z⊊Y)，则Z对X传递函数依赖，记作X-传递>Z

码（关键字，键）

简单来说，给定一个属性值，能够确定一行，就是候选码（给定张三和李四，可以分别确定二者所在的一行）

学号	姓名	…
001	张三
002	李四

若关系模式中有多个候选码，则选定其中的一个作为主码（一表一主码，主码可以为属性组）
关系模式R中，属性或属性组X并非R的码，但X是另一个关系模式的码，则X为R的外码

范式

5NF C 4NF C 3NF C 2NF C 1NF

1NF

二维表符合每个分量是不可分开的数据项的关系模式属于第一范式(1对1，合并单元格不符合定义)

2NF

R∈1NF，且每个非主属性都完全函数依赖与任何一个候选码，则R∈2NF
用于消除部分函数依赖

如何将1NF转化为2NF：
将部分函数依赖的非主属性单独建立一个表，然后加入一个码，使其与其他表联系起来

3NF

R∈1NF，若R中不存在码X、属性组Y以及非主属性Z，使得X->Y,Y->Z成立，则称R∈3NF
用于消除传递依赖

如何消除传递依赖：
将含传递依赖的表拆开。如（Sno,Sdept,Sloc）中，Sno->Sdept，Sdept->Sloc，将Sdept和Sloc拆开，成为(Sno,Sdept)，(Sdept,Sloc)

BCNF

认为是修正的第三范式
若R∈1NF，若X->Y，且Y⊊X时X必含有码(候选码也可以)，则R∈BCNF
换言之，如果每一个决定属性集都属于候选码

多值依赖

在关系数据库中，假设 R(A, B, C) 是一个表，其中 A、B、C 是属性，多值依赖表示为：如果属性 A 确定了属性集 B 的值，并且同时 A 确定了另一个属性集 C 的值，那么在给定的 A 的条件下，B 和 C 彼此独立，且它们的值可以是多对多的关系，写作A->->B（一对多，比如（CTB，课程C，教师T，参考书B））

平凡多值依赖
A->->B，B含于A
非平凡多值依赖
否则称为非平凡多值依赖

4NF

对于每个非平凡多值依赖X->->Y，若X都含有码则符合第四范式
第四范式仅允许存在非平凡多值依赖且为函数依赖但关系

如何将多值依赖转化为4NF：
假设有关系WSC，W->->S,w->->C,都是非平凡多值依赖，且W不是码，WSC的码为(W,S,C)，可以将WSC分解为WS(W,S)，WC(W,C)此时WS和WC都属于第四范式

数据依赖的公理系统

逻辑蕴含

设，对于满足一组函数依赖F的关系模式R<U,F>，存在X->A,X->B，且根据已有的函数依赖可以推出X->A∩B，成为F逻辑蕴含X->A∩B

Armstrong公理系统

推理规则

通俗的写：【X】【Y】【Z】都代表关系模式的子集

自反律：若Y是X的子集，则X→Y为F所蕴含
增广律：如果X→Y为F所蕴含，则XZ→YZ（X∪Z→Y∪Z）
传递律：如果X→Y，Y→Z为F所蕴含，则X→Z

根据上述三个规则可以推出以下规则

合并规则：由X->Y，X->Z，则X->YZ
伪传递规则：由X->Y，WY->Z，有XW->Z（替换）
分解规则：由X->Y，Z∈Y，有X->Z

闭包

函数依赖的闭包：
在关系模式R<U,F>中F所逻辑蕴含的函数依赖的全体叫做F的闭包，记作F+
属性的闭包：
设F为属性集U上的一组函数依赖，X、Y∈U，X+F={A|X->A能由Armstrong公理推出}，X+F称为属性集X关于函数依赖集F的闭包，即指所有能由X决定的属性集合

候选码的求解方法

属性的分类

L：仅出现在函数依赖集F左部的属性
R：…右部…
LR：…左右都出现…
N：…左右都未出现…

根据上述有以下结论：

若X是L类属性，则X必为R的任意候选码的成员（必定有一个候选码包含X）。若X+F=U，则X必为R的唯一候选码
若X是R类属性，则X不是R的任一候选码成员
若X是N类属性，则X必为R的任一候选码成员

求解方法

将所有属性分类
将所有L类和N类属性组合起来，设为P，求其闭包P+F，如果是全集U，则为候选码
如果不是全集U，则依次将LR类属性跟P组合起来求闭包，只要闭包是全集U，则为候选码

最小函数依赖集

如果函数依赖集F满足下列条件，则称F为一个最小函数依赖集，或称极小函数依赖集或最小覆盖。

F中的任一函数依赖的右部仅有一个属性，即无多余的属性
F中不存在这样的函数依赖X→A,使得F与F-{X-→A}等价，即无多余的函数依赖
F中不存在这样的函数依赖X→A,X有真子集Z使得F与F-{X→A]U{Z→A]等价，即去掉各函数依赖左边的多余属性。
即：
(1)所有函数依赖的右侧只有一个属性。
(2)没有冗余的函数依赖。
(3)所有函数依赖的左侧没有冗余的属性。

第七章——数据库设计

三个步骤：

概念设计——ER图
逻辑设计——确定关系模式
物理设计

概念设计和逻辑设计

实体(矩形表示)：现实中客观存在的
属性(椭圆表示)：每个实体固有的属性和特征
联系(菱形表示)：实体和实体间的联系
1. 一对一
2. 一对多对多端的关系模式来说，一端的主码需要放到多端合成关系模式；联系若有属性，则该属性需要放入多端才能合成关系模式
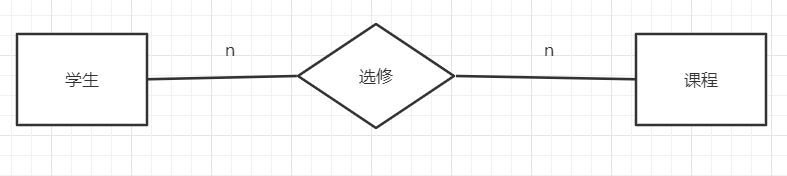3. 多对多联系需要取多端的主码+自己本身的属性才能合成关系模式